BM Research

Recently Syndicate Room published a fascinating study entitled Beating the Dragons How Radical Diversification can out perform VCs. This builds on the study they have been doing for the last couple of years (latest version here). Of special appeal to me was the use of Monte Carlo bootstrap methods to generate returns on simulated portfolios. Given my MSc students will be using Monte Carlo simulations next month, I’m kind of nerding out here.

I recommend reading the full study (its not too long) but I’ll summarise the methodology here. Using data from Beauhurst, the data consists of companies that raised seed or venture funding in 2011, with returns tracked to 2018. This gives 506 companies for which they either have exit values, including write-offs, or updated valuation information. Lots of simulations (100,000 were used per strategy) were done to generate portfolios of different sizes drawn from the sample. This is a well known method, but I commend Syndicate Room / Beauhurst for using it here.

And they have produced some fascinating results. I’m not going to produce the full results here, but I’ll give one example as it illustrates the points I want to make. If you want more then go read the study!

• 10 companies – return of 2.4x
• 30 companies – return of 3.7x
• 80 companies – return of 4.7x

These are returns over 7 years when investing in £500k – £5m rounds. Smaller rounds produced lower returns, but the pattern is the same.

I want to make three points about this: one is a point I think they have understated, one that I think they have missed and another that may actually be wrong.

Point 1: more companies give better returns

The study hardly ignores this point as its in the title, but it perhaps does not bring out what is going on here properly. The idea of a small number of companies producing the lion’s share of returns in venture capital is not new. Many top VCs in Silicon Valley, such as Peter Thiel and Marc Andreessen, have pointed out that venture capital returns follow some sort of power law.

Perhaps the most interesting, and clear, articulation of this has been by Jerry Neumann. In a blog post in 2015, he works through the implications of power law returns. The most powerful of these is that the greater the number of companies that you invest in, the higher your expected return.

The idea of larger numbers has also been discussed by Dave McClure at 500 Startups. He suggested 20-40 investments is far too small and 100-200 companies is appropriate for early-stage investments. So the numbers suggested in the study are not new or even that radical.

The weakness of this is that the power law is largely a hypothesis, albeit with some supporting evidence. This study adds to that evidence. Well done!

Point 2: what about risk?

One of the great things about the simulation method is that there is a wide range of portfolio returns which would allow some estimation of risk. Nowhere in the study do they do that. It is not irrelevant to compare returns. But it can be misleading to do so with an indication of the risk being taken. Even better, returns can be compared on a risk -adjusted basis. I might take a 10% p.a. return with no risk over a 15% p.a. return with very high risk.

The presence of power laws means that this is not a trivial issue to analyse. For example, for many power laws the standard deviation is not defined. Yes, the most common measure of risk doesn’t exist! I’ve seen failure rates suggested as an alternative, but this is an area ripe for development.

My guess would be that risk rises along with return in the portfolios. It may rise at a slower rate, which would be good. It may not, which would be bad. Or I may be wrong altogether. But risk should not be ignored.

Point 3: diversification beats the Dragons but maybe not VCs

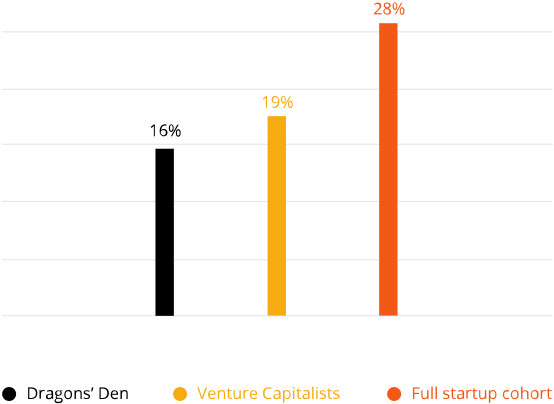
The headline is good and they give some justification for it. They quote annualised returns to Dragons of 16%, VCs 19% and the whole cohort of 28%. Stunning eh? Then they draw two conclusions:

• diversification can beat the Dragons. True.
• diversification can beat the VCs. Mmm, not convinced. Unproven at best!

So why is this? So it has been shown that bigger portfolios outperform smaller ones. The second statement is simply that the biggest portfolio outperforms a smaller one. Well the maths tells us that is going to happen, but it does not show “most venture capitalists would be better off picking their investments at random”. No. Not at all.

There’s another couple of strong caveats to this statement. The previous point mentioned risk. It may be that the VCs are doing better on a risk-adjusted basis. And one reason why this could be true is that capital-preservation EIS companies would be in the data. The problem is these targeted much lower returns than the averages in the simulations. It is also possible that the VC selection process reduces risk. Or it may not. But we need to take account of it.

Data issues too

The next issue is one about the data. Although the cohort analyses 506 companies, there were 676 that received investment in 2011. While I’ve been told there were some initial mis-classifications, the rest are excluded due to unreliable data. This suggests to me these are companies with issues, and a higher proportion may be effective wipeouts compared to the used sample. This would bring down the absolute return figures, but probably not break power law pattern.

However, if a VC is doing its job (maybe presumptuous, but not in my experience) then it’s investments are more likely to be in the sample with reliable data. This suggests the dampening due to these excluded companies will affect the overall portfolio return more than the VC one. By how much? No idea, but it may not be trivial given the number of excluded investments is a third of the existing dataset.

And one more point

I know I said three points, but this is not on the results, but how they might be applied. The statement for VCs implies that investments can be chosen at random and all will be fine. Not quite!

The results are for investment opportunities conditional on them having received investment. If investments are chosen at random from opportunities that are presented that may give different results.

Actually I’d suggest will give different results. Think about a Michael Maboussin idea for deciding whether luck or skill dominates in a investment. Ask yourself how easy is to do badly? For quoted companies its not that easy. In start-ups it is almost trivially easy. This suggests that just picking investment opportunities at random is a really bad idea! But you knew that already.

Final comment

While its easy to be critical, I think Syndicate Room and Beauhurst have done a great job in producing this study. My hope is by writing this I can help generate some debate about these ideas, not undermine them. I’ve been writing about them for my book and maybe will put that out at some point too.